Análise de PERT/CPM - Incertezas nas durações das atividades#
Conforme visto, o método PERT (Program Evaluation and Review Technique) é uma técnica de gerenciamento de projetos que considera a incerteza nas durações das atividades. A técnica utiliza três estimativas: otimista (o), mais provável (m) e pessimista (p). A partir dessas estimativas, calcula-se a média (\(\mu\)) e a variância (\(\sigma^2\)) de cada atividade, permitindo uma melhor previsão dos prazos do projeto, mesmo diante de incertezas. Essa abordagem, combinada com o CPM (Critical Path Method), auxilia na identificação do caminho crítico, ou seja, a sequência de atividades que determina a duração mínima do projeto.
As fórmulas utilizadas no cálculo são: Aqui estão as fórmulas em LaTeX adequadas para Markdown:
Duração esperada (\(\mu\)):
[ \(\mu = \frac{o + 4m + p}{6}\) ]Variância (\(\sigma^2\)):
[ \(\sigma^2 = \left( \frac{p - o}{6} \right)^2\) ]
import pandas as pd
from fractions import Fraction
# Dados de entrada (sem as colunas Média e Variância)
data = {
'Atividade': ['Início', 'A', 'B', 'C', 'D',
'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'Fim'],
'Descrição': ['Início', 'Escavação', 'Fundação', 'Paredes', 'Telhado',
'Encanamento<br>Exterior', 'Encanamento<br>Interior', 'Muros',
'Pintura<br>Exterior', 'Instalação<br>Elétrica', 'Divisórias', 'Piso',
'Pintura<br>Interior', 'Acabamento<br>Exterior', 'Acabamento<br>Interior', 'Fim'],
#'Atividades Precedentes': [None, 'Início', 'A', 'B', 'C', 'C', 'E', 'D', 'E,G', 'C', 'F,I', 'J', 'J', 'H', 'K,L', 'M,N'],
'Duração Estimada': [0, 2, 4, 10, 6, 4, 5, 7, 9, 7, 8, 4, 5, 2, 6, 0],
'o': [None, 1, 2, 6, 4, 1, 4, 5, 5, 3, 3, 4, 1, 1, 5, None],
'm': [None, 2, 3.5, 9, 5.5, 4.5, 4, 6.5, 8, 7.5, 9, 4, 5.5, 2, 5.5, None],
'p': [None, 3, 8, 18, 10, 5, 10, 11, 17, 9, 9, 4, 7, 3, 9, None]
}
# Função para calcular a média e a variância
def calculate_mean_variance(o, m, p):
if pd.isna(o) or pd.isna(m) or pd.isna(p):
return None, None
# Média: (o + 4m + p) / 6
mean = (o + 4 * m + p) / 6
# Variância: ((p - o) / 6) ** 2
variance = ((p - o) / 6) ** 2
# Converter variância para fração mínima
variance_fraction = str(Fraction(variance).limit_denominator())
return mean, variance_fraction
# Criar o DataFrame com o cálculo da média e variância no momento da criação
df = pd.DataFrame(data)
# Calcular a média e a variância para cada linha
df['Média'], df['Variância'] = zip(*df.apply(lambda row: calculate_mean_variance(row['o'], row['m'], row['p']), axis=1))
# Exibindo o DataFrame com formatação HTML (para mostrar as quebras de linha corretamente)
from IPython.display import display, HTML
# Exibindo o DataFrame com HTML
display(HTML(df.to_html(escape=False)))
Além dos caminhos que consideram a média do projeto, considerando as estimativas pessimistas e otimistas, é possível calcular o pior e o melhor cenário.
import pandas as pd
import networkx as nx
from IPython.core.display import display, HTML
# Criar o DataFrame com as informações das atividades
data = pd.DataFrame({
'Atividade': ['Início', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'Fim'],
'Descrição': ['Início','Escavação', 'Fundação', 'Paredes', 'Telhado', 'Encanamento Exterior',
'Encanamento Interior', 'Muros', 'Pintura Exterior', 'Instalação Elétrica', 'Divisórias',
'Piso', 'Pintura Interior', 'Acabamento Exterior', 'Acabamento Interior', 'Fim'],
'Atividades Precedentes': [None, 'Início', 'A', 'B', 'C', 'C', 'E', 'D', 'E,G', 'C', 'F,I', 'J', 'J', 'H', 'K,L', 'M,N'],
'Duração Estimada': [0, 2, 4, 10, 6, 4, 5, 7, 9, 7, 8, 4, 5, 2, 6, 0],
'Duração Otimista': [0, 1, 2, 6, 4, 1, 4, 5, 5, 3, 3, 4, 1, 1, 5, 0],
'Duração Pessimista': [0, 3, 8, 18, 10, 5, 10, 11, 17, 9, 9, 4, 7, 3, 9, 0]
})
# Função para calcular os caminhos e destacar o caminho crítico
def calculate_paths_and_critical(data, duration_column, highlight_color):
G = nx.DiGraph()
# Adicionar nós e arestas ao grafo com base na coluna de duração especificada
for i, row in data.iterrows():
G.add_node(row['Atividade'], duração=row[duration_column])
if row['Atividades Precedentes']:
precedentes = row['Atividades Precedentes'].split(',')
for p in precedentes:
G.add_edge(p.strip(), row['Atividade'])
# Função para encontrar todos os caminhos do início ao fim
def find_paths(graph, start, end, path=[]):
path = path + [start]
if start == end:
return [path]
if start not in graph:
return []
paths = []
for node in graph[start]:
if node not in path:
new_paths = find_paths(graph, node, end, path)
for p in new_paths:
paths.append(p)
return paths
# Encontrar todos os caminhos do "Início" para "Fim"
all_paths = find_paths(G, 'Início', 'Fim')
# Calcular a duração de cada caminho
path_durations = []
for path in all_paths:
duration = sum(G.nodes[node]['duração'] for node in path)
path_durations.append((path, duration))
# Criar uma tabela com os caminhos e suas durações
paths_df = pd.DataFrame(path_durations, columns=['Caminho', 'Duração Total'])
paths_df['Caminho'] = paths_df['Caminho'].apply(lambda x: ' -> '.join(x)) # Formatar o caminho como uma string
# Encontrar o caminho crítico (o de maior duração)
critical_path, critical_duration = max(path_durations, key=lambda x: x[1])
# Função para destacar o caminho crítico na cor especificada
def highlight_critical(path):
return ' -> '.join(
[f"<span style='color:{highlight_color}'>{node}</span>" if node in critical_path else node for node in path]
)
# Destacar o caminho crítico e a duração total na tabela
paths_df['Caminho'] = paths_df['Caminho'].apply(lambda x: highlight_critical(x.split(' -> ')))
paths_df['Duração Total'] = paths_df['Duração Total'].apply(
lambda x: f"<span style='color:{highlight_color}'><b>{x}</b></span>" if x == critical_duration else x
)
# Retornar o DataFrame formatado
return paths_df
# Tabela para a duração otimista (destacado em azul)
optimistic_paths_df = calculate_paths_and_critical(data, 'Duração Otimista', 'blue')
# Tabela para a duração estimada (destacado em verde)
estimated_paths_df = calculate_paths_and_critical(data, 'Duração Estimada', 'green')
# Tabela para a duração pessimista (destacado em vermelho)
pessimistic_paths_df = calculate_paths_and_critical(data, 'Duração Pessimista', 'red')
# Exibir as tabelas
display(HTML("<h3>Duração Otimista</h3>"))
display(HTML(optimistic_paths_df.to_html(escape=False)))
display(HTML("<h3>Duração Estimada</h3>"))
display(HTML(estimated_paths_df.to_html(escape=False)))
display(HTML("<h3>Duração Pessimista</h3>"))
display(HTML(pessimistic_paths_df.to_html(escape=False)))
Distribuição Normal e Cálculo da Probabilidade#
A distribuição normal pode ser utilizada para modelar o tempo total de um projeto no contexto do PERT/CPM, considerando as incertezas nas durações das atividades. Ela é caracterizada pela média (\(\mu\)), que representa o tempo esperado do projeto, e o desvio padrão (\(\sigma\)), que reflete a variabilidade no tempo de conclusão do projeto. O desvio padrão total do caminho crítico é calculado somando as variâncias das atividades nesse caminho.
A probabilidade de concluir o projeto em um tempo \(T\) é dada pela função de distribuição acumulada normal (CDF):
\( P(T) = P(X \leq T) = \Phi\left( \frac{T - \mu_p}{\sigma_p} \right) \)
Onde:
\(\Phi\) é a função de distribuição acumulada da normal.
\(\mu_p\) é a média do tempo total do caminho crítico.
\(\sigma_p\) é o desvio padrão do caminho crítico, calculado pela raiz quadrada da soma das variâncias das atividades no caminho crítico.
\(T\) é o tempo fornecido para calcular a probabilidade.
O desvio padrão do caminho crítico é calculado por:
\( \sigma_p = \sqrt{\sum_{i=1}^{n} \sigma_i^2} \)
Onde \(\sigma_i^2\) é a variância de cada atividade no caminho crítico, e \(n\) é o número de atividades nesse caminho.
import math
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
from fractions import Fraction
# Função para calcular a probabilidade
def calcular_probabilidade(mu_p, variancia_atividades, T):
# Passo 1: Calcular o desvio padrão total (σ_p)
sigma_p = math.sqrt(sum(variancia_atividades))
# Passo 2: Calcular o número de desvios padrão (k_a)
k_a = (T - mu_p) / sigma_p
# Passo 3: Calcular a probabilidade usando a distribuição normal
probabilidade = norm.cdf(k_a) # Função de distribuição acumulada da normal
return probabilidade, sigma_p, k_a
# Função para converter frações em números decimais
def fração_para_decimal(fração_str):
try:
return float(Fraction(fração_str.strip()))
except ValueError:
print(f"Erro ao converter a fração: {fração_str}. Certifique-se de usar o formato correto, como '1/9'.")
return 0.0
# Solicitar ao usuário a duração total do Caminho Crítico e as variâncias das atividades
mu_p = float(input("Informe a duração total do Caminho Crítico (μ_p) em unidades de tempo: ")) # Exemplo anterior: Caminho crítico Médio: Início -> A -> B -> C -> E -> F -> J -> L -> N -> Fim: 44
variancia_atividades = list(map(fração_para_decimal, input("Informe as variâncias das atividades separadas por vírgula (por exemplo, '1/9'): ").split(','))) # Exemplo anterior atividades: 1/9, 1, 4, 4/9, 1, 1, 1, 4/9
# Solicitar o tempo T para calcular a probabilidade
T = float(input("Informe a duração do projeto (T) para calcular a probabilidade: ")) # Exemplo anterior o desvio padrão é 3
# Calcular a probabilidade
probabilidade, sigma_p, k_a = calcular_probabilidade(mu_p, variancia_atividades, T)
# Exibir o resultado
print(f"A probabilidade de o projeto ser completado em {T} unidades de tempo é: {probabilidade:.4f}")
# Gerar o gráfico da distribuição normal
x = np.linspace(mu_p - 4*sigma_p, mu_p + 4*sigma_p, 1000)
y = norm.pdf(x, mu_p, sigma_p)
plt.figure(figsize=(10, 6))
# Plotar a distribuição normal
plt.plot(x, y, label="Distribuição Normal", color='blue')
# Destacar a área da probabilidade em amarelo
x_fill = np.linspace(mu_p - 4*sigma_p, T, 1000)
y_fill = norm.pdf(x_fill, mu_p, sigma_p)
plt.fill_between(x_fill, y_fill, color='yellow', alpha=0.5, label=f'Área até T = {T}')
# Adicionar marcação de T
plt.axvline(x=T, color='red', linestyle='--', label=f'T = {T}')
# Adicionar títulos e rótulos
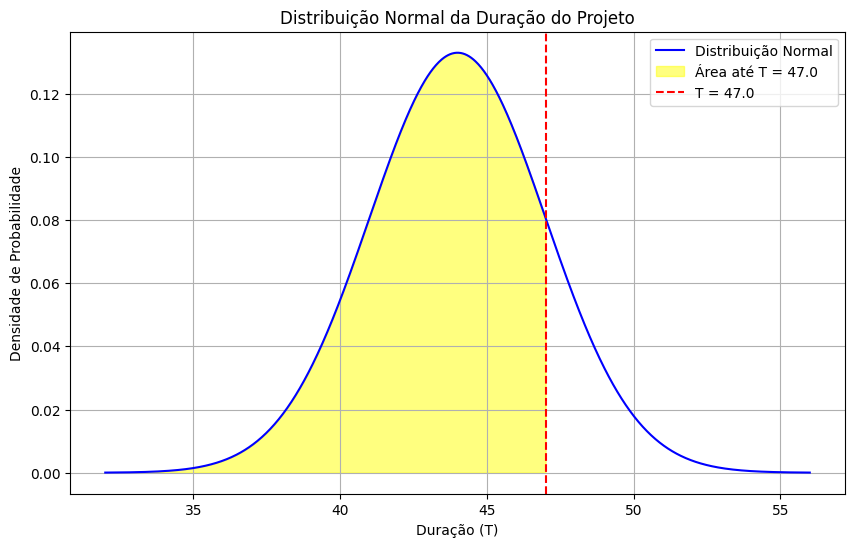
plt.title('Distribuição Normal da Duração do Projeto')
plt.xlabel('Duração (T)')
plt.ylabel('Densidade de Probabilidade')
plt.legend()
# Exibir o gráfico
plt.grid(True)
plt.show()
A probabilidade de o projeto ser completado em 47.0 unidades de tempo é: 0.8413