Ações de correção para situações de atenção#

Abaixo, apresentamos um exemplo ilustrativo abordando a situação 1 (pontos fora dos limites de controle), incluindo explicações, ferramentas de análise como Diagrama de Causa e Efeito, e a aplicação das técnicas de CEP e PMBOK para o gerenciamento e resolução do problema.

Situação 1: Pontos Fora do Limite de Controle#

Contexto:#

Imagine que estamos monitorando a resistência do concreto em uma obra da construção civil. A resistência ideal do concreto é definida como 30 MPa, e o desvio padrão esperado é 2 MPa. Durante os testes diários, alguns pontos de medição começam a exceder os limites superiores ou inferiores de controle, indicando um possível problema no processo de produção do concreto.

Exemplo de Código - Situação 1: Este código cria um gráfico que mostra a resistência do concreto em 30 amostras, com alguns pontos fora dos limites de controle definidos.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Definições
n_amostras = 30
media = 30  # Resistência média do concreto (MPa)
desvio_padrao = 2  # Desvio padrão esperado (MPa)
LC_superior = media + 3 * desvio_padrao  # Limite superior de controle
LC_inferior = media - 3 * desvio_padrao  # Limite inferior de controle

# Gerando os dados de resistência do concreto com alguns pontos fora de controle
dados = np.random.normal(media, desvio_padrao, n_amostras)
dados[5] = 40  # Ponto acima do limite superior
dados[15] = 10  # Ponto abaixo do limite inferior

# Criando o DataFrame
df = pd.DataFrame({'Dia': range(1, n_amostras + 1), 'Resistência (MPa)': dados})

# Plotando os gráficos
plt.figure(figsize=(10,6))
plt.plot(df['Dia'], df['Resistência (MPa)'], marker='o', color='b', label='Resistência Observada')
plt.axhline(media, color='g', linestyle='--', label='Média Ideal (25 MPa)')
plt.axhline(LC_superior, color='r', linestyle='--', label='Limite Superior (31 MPa)')
plt.axhline(LC_inferior, color='r', linestyle='--', label='Limite Inferior (19 MPa)')

# Destacando os pontos fora de controle
plt.scatter([6, 16], [40, 10], color='red', zorder=5, label='Pontos Fora de Controle')

plt.title('Controle Estatístico de Processo: Resistência do Concreto')
plt.xlabel('Dia')
plt.ylabel('Resistência (MPa)')
plt.legend(loc='upper right')
plt.grid(True)
plt.show()

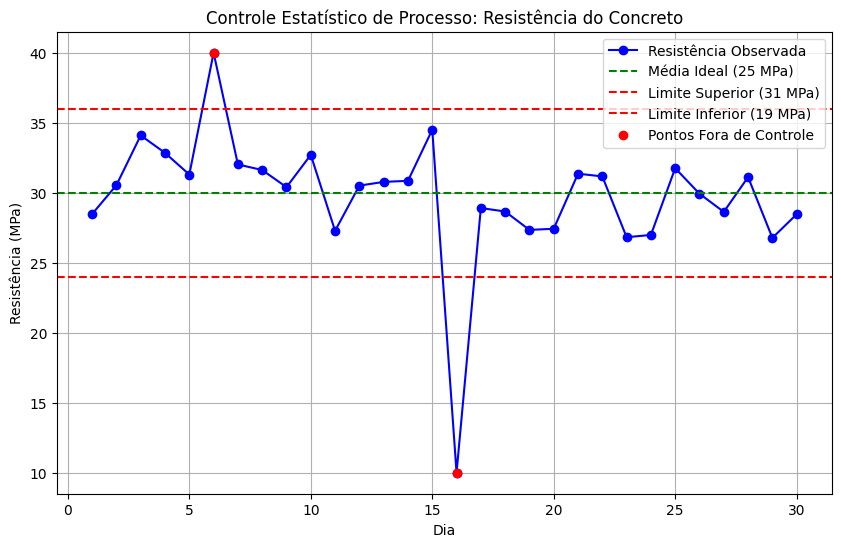
Gráfico Gerado:

• O gráfico acima mostra os pontos de resistência do concreto ao longo de 30 dias. O ponto em 6º dia (40 MPa) está acima do limite superior, e o ponto no 16º dia (10 MPa) está abaixo do limite inferior.

O que o Gerente de Projeto Deve Fazer?#

1. Análise de Dados

   • O gerente deve analisar a distribuição dos dados e identificar se a variação é aceitável ou se os pontos fora dos limites de controle indicam um problema real no processo de produção do concreto.

   • Limites de Controle: No gráfico acima, os limites de controle são definidos como LC Superior (36 MPa) e LC Inferior (24 MPa). O fato de termos pontos fora desses limites pode indicar que o processo está fora de controle e necessita de investigação.

2. Causas Possíveis

   • Causa de falha no processo:

     • O controle inadequado da mistura pode resultar em resistência do concreto fora dos padrões.

     • Falha no equipamento de medição ou defeito no material (por exemplo, variação nos componentes do concreto).

     • Erro humano durante a medição ou preparação da mistura.

   Ferramenta de Análise: Diagrama de Causa e Efeito (Ishikawa)

   O gerente pode criar um diagrama para investigar as causas potenciais das falhas.

import matplotlib.pyplot as plt

def plot_ishikawa_optimized():
    fig, ax = plt.subplots(figsize=(14, 8))

    # Linha central com o efeito no lado direito
    ax.plot([-12, 0], [0, 0], color="black", lw=2)  # Linha horizontal central
    ax.arrow(0, 0, 0.3, 0, head_width=0.2, head_length=0.4, fc='black', ec='black')

    # Adicionar as espinhas para as causas
    # Causas na parte superior
    ax.plot([-3, -5], [0, 2], color="black", lw=2)  # Erro Humano
    ax.plot([-7, -9], [0, 2], color="black", lw=2)  # Equipamento de Medição
    # Causas na parte inferior
    ax.plot([-3, -5], [0, -2], color="black", lw=2)  # Mistura de Concreto
    ax.plot([-7, -9], [0, -2], color="black", lw=2)  # Controle de Qualidade

    # Textos das causas
    ax.text(-5.5, 2.3, "Erro Humano", fontsize=12, va="center", ha="center", weight='bold')
    ax.text(-9.5, 2.3, "Equipamento de Medição", fontsize=12, va="center", ha="center", weight='bold')
    ax.text(-5.5, -2.3, "Mistura de Concreto", fontsize=12, va="center", ha="center", weight='bold')
    ax.text(-9.5, -2.3, "Controle de Qualidade", fontsize=12, va="center", ha="center", weight='bold')

    # Texto do efeito
    ax.text(1, 0, "Resistência do Concreto", fontsize=14, va="center", ha="left", weight='bold')

    # Ajustes do gráfico
    ax.set_xlim([-13, 2])
    ax.set_ylim([-3, 3])
    ax.axis('off')  # Desativa os eixos

    plt.show()

# Gerar o Diagrama de Ishikawa otimizado
plot_ishikawa_optimized()

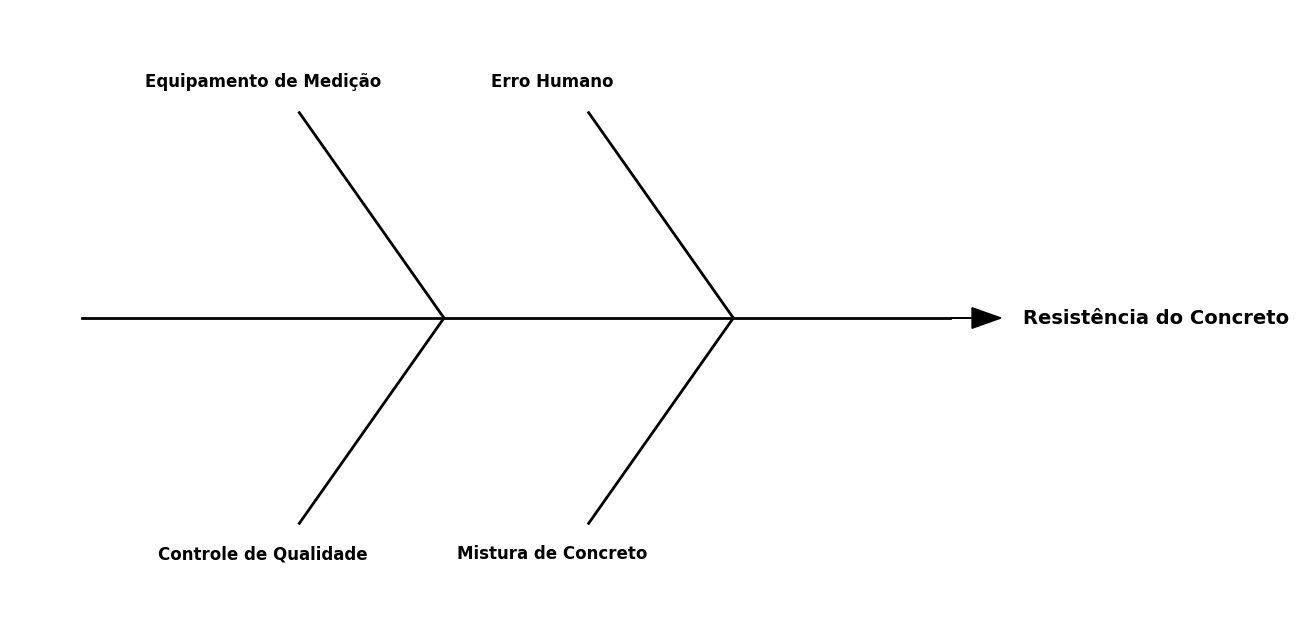
Ações Corretivas e Preventivas#

O gerente de projeto, ao identificar as causas da falha, deve aplicar as seguintes ações de correção e prevenção:

• Correção Imediata:

  • Verificar os pontos de controle de qualidade e equipamentos de medição. Garantir que as medições de resistência sejam precisas.

  • Se necessário, ajustar a mistura de concreto para garantir que a resistência esteja dentro dos limites esperados.

• Ações Preventivas:

  • Treinamento contínuo para a equipe sobre as práticas de controle de qualidade.

  • Auditorias periódicas nos processos de produção e medição para garantir que o processo esteja sempre sob controle.

  • Melhoria contínua no processo, utilizando dados de monitoramento para ajustar e otimizar os parâmetros de produção.

Após a análise com o Diagrama de Causa e Efeito (Ishikawa), podemos aplicar outras técnicas importantes de controle de qualidade, como Análise de Pareto e Formulários de Análise de Causa.

Técnicas de Controle de Qualidade:#

1. Análise de Pareto#

A Análise de Pareto segue o princípio 80/20, onde 80% dos problemas podem ser causados por 20% das causas. No nosso exemplo, podemos usar essa técnica para identificar quais fatores têm maior impacto nas falhas do processo de produção do concreto. Se, por exemplo, a maioria das falhas for causada por problemas de mistura de concreto ou erro humano, isso deve ser priorizado nas ações corretivas.

Como aplicar:

• Primeiro, coletamos os dados sobre as falhas (como tipo de falha: mistura, equipamento, erro humano).

• Então, organizamos esses dados de forma decrescente de frequência e calculamos a contribuição percentual de cada causa.

Exemplo de Código - Análise de Pareto:

import pandas as pd
import matplotlib.pyplot as plt

# Exemplo de causas e ocorrências de falhas
dados_causas = {'Causa': ['Erro Humano', 'Mistura de Concreto', 'Equipamento de Medição', 'Controle de Qualidade', 'Fatores Externos'],
                'Ocorrências': [7, 10, 4, 3, 2]}

# Criação do DataFrame
df_causas = pd.DataFrame(dados_causas)

# Ordenando por ocorrências
df_causas = df_causas.sort_values('Ocorrências', ascending=False)

# Cálculo da contribuição percentual acumulada
df_causas['Contribuição %'] = 100 * df_causas['Ocorrências'].cumsum() / df_causas['Ocorrências'].sum()

# Plotando o gráfico de Pareto
fig, ax1 = plt.subplots(figsize=(10,6))

# Barras para as ocorrências
ax1.bar(df_causas['Causa'], df_causas['Ocorrências'], color='b', alpha=0.6)
ax1.set_xlabel('Causa')
ax1.set_ylabel('Ocorrências', color='b')

# Linha para contribuição percentual acumulada
ax2 = ax1.twinx()
ax2.plot(df_causas['Causa'], df_causas['Contribuição %'], color='r', marker='o', label='Contribuição Acumulada %')
ax2.set_ylabel('Contribuição Acumulada (%)', color='r')

# Título e exibição
plt.title('Análise de Pareto: Causas das Falhas no Processo de Concreto')
ax2.legend(loc='upper left')
plt.show()

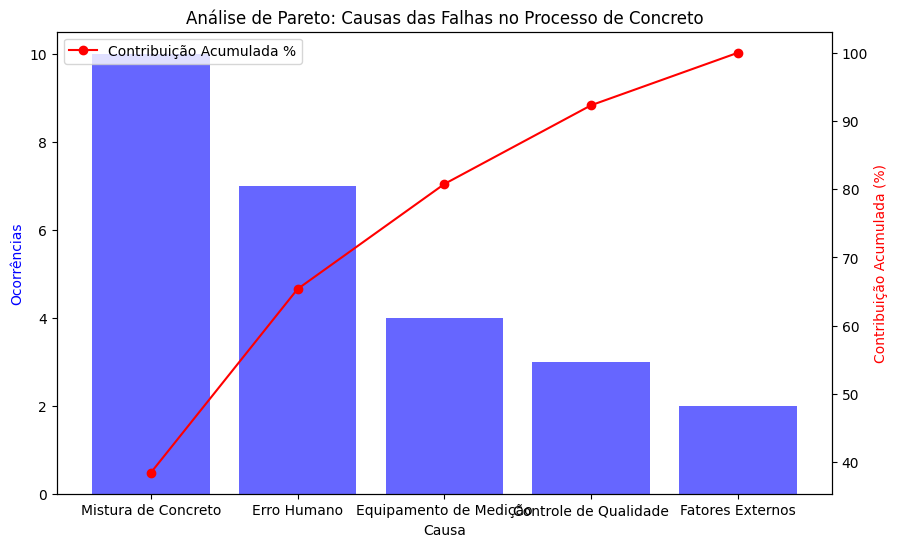
Gráfico Gerado:

• O gráfico de Pareto nos permite visualizar quais causas estão contribuindo mais para as falhas. Se, por exemplo, a Mistura de Concreto representar a maior parte das falhas (mais de 80%), isso deve ser o foco da ação corretiva.

# Cálculo do CPK
limite_inferior = media - 3 * desvio_padrao
limite_superior = media + 3 * desvio_padrao

# Cálculo do CPK
cpk = min((LC_superior - media) / (3 * desvio_padrao), (media - LC_inferior) / (3 * desvio_padrao))
cpk

1.0

Ações de Correção e Melhoria#

Com as ferramentas e cálculos acima, o gerente pode:

1. Identificar as Causas Prioritárias: Usando a Análise de Pareto, o gerente deve focar na causa que tem maior impacto (por exemplo, Mistura de Concreto).

2. Implementar Ações Corretivas: Se a causa principal for uma mistura inadequada, é necessário rever as proporções dos materiais, ajustar o processo e fazer treinamentos com a equipe para garantir o controle adequado.

3. Monitorar e Controlar o Processo: Usar SPC para monitorar continuamente o processo e garantir que os pontos de controle (como resistência do concreto) estejam dentro dos limites aceitáveis. Isso pode ser feito com gráficos de controle atualizados constantemente.

4. Ações Preventivas: Usar o FMEA para antecipar possíveis falhas e desenvolver planos de ação para prevenir essas falhas em futuras produções de concreto.

Conclusão#

Ao aplicar técnicas como Análise de Pareto, FMEA, e Controle Estatístico de Processo (CEP), aliados às práticas do PMBOK, o gerente de projeto pode identificar, corrigir e prevenir falhas na produção de concreto, assegurando que o material atenda aos padrões de resistência necessários. Ferramentas como gráficos de controle, Diagrama de Causa e Efeito, e a implementação de ações corretivas e preventivas permitem uma resposta rápida a falhas e promovem a melhoria contínua, garantindo a qualidade e a segurança do processo de construção civil.