1. O que é uma simulação de Monte Carlo?#

A simulação de Monte Carlo é uma técnica estatística usada para modelar incertezas. Ela funciona ao realizar múltiplas iterações (ou simulações) com valores aleatórios gerados para variáveis incertas, a fim de prever um intervalo de possíveis resultados.

No caso de engenharia civil, ela pode ser aplicada, por exemplo, para estimar custos de projetos, duração de atividades ou riscos de atrasos, considerando incertezas inerentes a essas variáveis.

2. Definição do Problema#

No exemplo fornecido:

• Estamos simulando o custo total de um projeto de construção.

• Consideramos três componentes principais de custo:

  1. Materiais: custo dos materiais com uma distribuição normal (com média e desvio padrão).

  2. Mão de obra: custo da mão de obra com uma distribuição triangular (com valores mínimo, máximo e mais provável).

  3. Equipamentos: custo dos equipamentos com uma distribuição uniforme (entre um intervalo fixo).

O objetivo é realizar várias iterações para calcular o custo total do projeto, levando em conta a aleatoriedade das variáveis.

3. Descrição do Código#

import numpy as np
import matplotlib.pyplot as plt

# Parâmetros para os custos de materiais
mean_materials = 50000
std_dev_materials = 5000

# Parâmetros para os custos de mão de obra
min_labor = 30000
most_likely_labor = 40000
max_labor = 60000

# Parâmetros para os custos de equipamentos
min_equip = 20000
max_equip = 30000

num_simulations = 10000
total_costs = []

for _ in range(num_simulations):
    materials = np.random.normal(mean_materials, std_dev_materials)
    labor = np.random.triangular(min_labor, most_likely_labor, max_labor)
    equipment = np.random.uniform(min_equip, max_equip)
    total_cost = materials + labor + equipment
    total_costs.append(total_cost)

mean_cost = np.mean(total_costs)
percentile_5 = np.percentile(total_costs, 5)
percentile_95 = np.percentile(total_costs, 95)

plt.hist(total_costs, bins=50, color='blue', alpha=0.7)

4. Aplicação Prática na Engenharia Civil#

• Este exemplo simula incertezas no custo de materiais, mão de obra e equipamentos.

• O intervalo de confiança (percentis) é útil para planejar orçamentos considerando incertezas, permitindo:

  • Planejamento de contingências: reservar fundos para cenários mais caros.

  • Mitigação de riscos financeiros: identificar os maiores fatores de impacto no custo e planejar respostas.

Com a simulação de Monte Carlo, engenheiros e gestores podem tomar decisões mais informadas, minimizando surpresas financeiras durante a execução do projeto.

Exemplo (Resumo): Estimativa de custos de construção#

1. Entradas principais:

   • Custos de materiais (com variação aleatória).

   • Custos de mão de obra (com variação aleatória).

   • Custos indiretos (fixos).

2. Saída esperada:

   • Estimativa do custo total, considerando as incertezas.

Explicação#

1. Distribuição Normal:

   • Os custos de materiais e mão de obra são modelados como distribuições normais, com médias e desvios padrão estimados.

2. Simulação:

   • O custo total é a soma dos custos simulados para materiais, mão de obra e custos fixos.

3. Análise Estatística:

   • Cálculo de estatísticas como média, desvio padrão, e intervalos de confiança (5% e 95%).

4. Visualização:

   • Um histograma apresenta a distribuição dos custos simulados.

Este exemplo pode ser facilmente adaptado para incluir outros custos ou diferentes distribuições de probabilidade, dependendo da complexidade do projeto.

import numpy as np
import matplotlib.pyplot as plt

# Parâmetros de entrada
n_simulations = 10000  # Número de simulações
material_cost_mean = 500000  # Custo médio dos materiais (R$)
material_cost_std = 50000    # Desvio padrão do custo dos materiais (R$)
labor_cost_mean = 300000     # Custo médio da mão de obra (R$)
labor_cost_std = 30000       # Desvio padrão do custo da mão de obra (R$)
indirect_cost = 100000       # Custos indiretos fixos (R$)

# Simulação de Monte Carlo
material_costs = np.random.normal(material_cost_mean, material_cost_std, n_simulations)
labor_costs = np.random.normal(labor_cost_mean, labor_cost_std, n_simulations)
total_costs = material_costs + labor_costs + indirect_cost

# Estatísticas dos resultados
mean_cost = np.mean(total_costs)
std_cost = np.std(total_costs)
percentile_5 = np.percentile(total_costs, 5)
percentile_95 = np.percentile(total_costs, 95)

# Exibição dos resultados
print(f"Estimativa do custo total (Monte Carlo):")
print(f"Custo médio: R$ {mean_cost:,.2f}")
print(f"Desvio padrão: R$ {std_cost:,.2f}")
print(f"Percentil 5%: R$ {percentile_5:,.2f}")
print(f"Percentil 95%: R$ {percentile_95:,.2f}")

# Visualização dos resultados
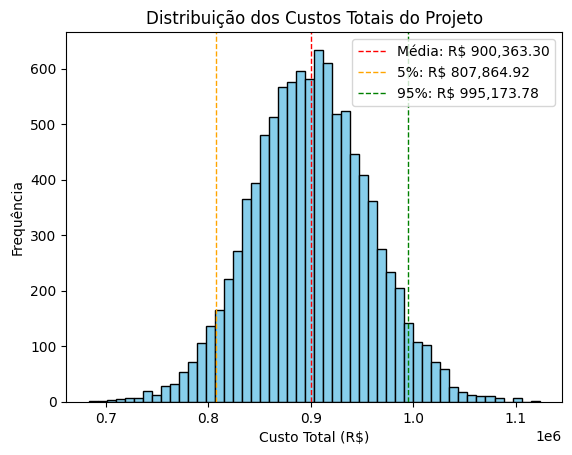
plt.hist(total_costs, bins=50, color='skyblue', edgecolor='black')
plt.axvline(mean_cost, color='red', linestyle='dashed', linewidth=1, label=f'Média: R$ {mean_cost:,.2f}')
plt.axvline(percentile_5, color='orange', linestyle='dashed', linewidth=1, label=f'5%: R$ {percentile_5:,.2f}')
plt.axvline(percentile_95, color='green', linestyle='dashed', linewidth=1, label=f'95%: R$ {percentile_95:,.2f}')
plt.title("Distribuição dos Custos Totais do Projeto")
plt.xlabel("Custo Total (R$)")
plt.ylabel("Frequência")
plt.legend()
plt.show()

Estimativa do custo total (Monte Carlo):
Custo médio: R$ 900,363.30
Desvio padrão: R$ 57,247.81
Percentil 5%: R$ 807,864.92
Percentil 95%: R$ 995,173.78