Introdução ao Controle Estatístico de Processos (CEP) e Gráficos de Controle#
O CEP é uma ferramenta fundamental para monitoramento de processos, e o PMBOK 7ª edição destaca a importância de medir e avaliar o desempenho de um projeto de forma contínua. O objetivo é garantir que o projeto está no caminho certo e que as variações nos processos sejam identificadas e corrigidas.
No contexto de Medição e Avaliação do Desempenho, o PMBOK 7ª edição aborda a importância de coletar dados, analisar o desempenho do projeto e usar essas informações para tomar decisões informadas. O CEP fornece um conjunto robusto de ferramentas para essa coleta e análise, como gráficos de controle, que ajudam a monitorar a variação nos processos de produção ou execução e tomar ações corretivas quando necessário.
Outras características do CEP relacionados a GPC:
Gráficos de Controle (como o gráfico de controle de média, desvio padrão ou proporção defeituosa) são exemplos claros de como o CEP pode ser utilizado para monitorar a qualidade e a variabilidade dos processos.
O CEP utiliza dados reais do processo para avaliar se o desempenho está dentro dos limites de controle e, se necessário, tomar ações corretivas, o que é essencial para a gestão de qualidade e desempenho em qualquer tipo de projeto.
O PMBOK 7ª edição foca em dados e análise contínua para a tomada de decisões baseadas em informações concretas, o que se alinha diretamente aos princípios do CEP.
Portanto, a conexão entre o CEP e a Medição e Avaliação do Desempenho no PMBOK é bastante forte, já que ambos lidam com a coleta de dados e análise para garantir que os processos do projeto estejam funcionando conforme o esperado, com a detecção de problemas antes que se tornem críticos.
1.1 O que é Controle Estatístico de Processos (CEP)?#
O Controle Estatístico de Processos (CEP) é uma metodologia usada para monitorar e controlar a qualidade de um processo de produção. Seu objetivo é garantir que o processo opere de forma eficiente, sem falhas ou desvios indesejados. Isso é feito medindo variáveis do processo e analisando sua variabilidade [GS12]
1.2 Tipos de Variação#
Em um processo de produção, as variações podem ser de dois tipos:
Variação Comum (ou Natural): Resulta de causas aleatórias, que são inerentes ao processo. Essas variações não são evitáveis e devem ser controladas com técnicas de melhoria contínua.
Variação Especial (ou Anômala): Causada por fatores fora do controle do processo. Essas variações podem ser identificadas e corrigidas.
1.3 Exemplos na Construção Civil#
Na construção civil, podemos usar o CEP para monitorar a qualidade de diversos processos, como:
Medição da espessura do concreto: É importante garantir que a espessura do concreto em uma fundação esteja dentro dos limites estabelecidos para garantir a segurança estrutural.
Controle de resistência do concreto: Verificar se a resistência do concreto está dentro das especificações, o que é crucial para a durabilidade e segurança das estruturas.
1.4 Gráficos de Controle#
Os gráficos de controle são ferramentas essenciais do CEP, usadas para monitorar como as medições de um processo variam ao longo do tempo. Eles ajudam a identificar quando um processo está fora de controle (quando a variação é anômala).
Os principais gráficos de controle usados são:
Gráfico de Controle de Média (X-bar): Usado para monitorar a média de uma variável (ex: resistência média do concreto).
Gráfico de Controle de Desvio Padrão (S): Usado para monitorar a variabilidade de uma variável (ex: variação na espessura do concreto).
1.5 Construindo um Gráfico de Controle de Média (X-bar)#
Passos:
Coletamos amostras do processo (por exemplo, 5 medições de resistência do concreto por dia).
Calculamos a média de cada amostra.
Calculamos a média geral e os limites de controle superior (UCL) e inferior (LCL) usando a fórmula de 3 desvios padrão.
Exemplo de Código - Gráfico de Controle de Média (X-bar)#
import numpy as np
import matplotlib.pyplot as plt
# Gerando dados simulados (resistência do concreto em MPa)
np.random.seed(42)
dados = np.random.normal(loc=30, scale=2, size=(20, 5)) # 20 amostras de 5 medições
# Calculando a média de cada amostra
medias = np.mean(dados, axis=1)
# Calculando a média geral
media_geral = np.mean(medias)
# Calculando o desvio padrão das amostras
desvio_padrao = np.std(medias)
# Calculando os limites de controle (UCL e LCL)
UCL = media_geral + 3 * desvio_padrao
LCL = media_geral - 3 * desvio_padrao
# Plotando o gráfico de controle
plt.figure(figsize=(10, 6))
plt.plot(medias, marker='o', label="Média das amostras")
plt.axhline(media_geral, color='green', linestyle='--', label="Média Geral")
plt.axhline(UCL, color='red', linestyle='--', label="Limite Superior de Controle (UCL)")
plt.axhline(LCL, color='red', linestyle='--', label="Limite Inferior de Controle (LCL)")
plt.title("Gráfico de Controle de Média (X-bar) - Resistência do Concreto")
plt.xlabel("Amostra")
plt.ylabel("Média da Resistência (MPa)")
plt.legend()
plt.show()
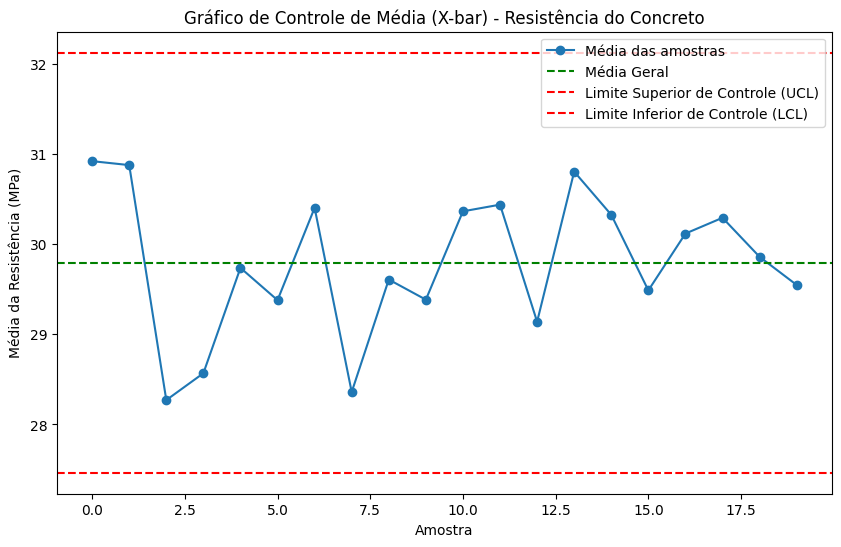
Explicação do gráfico:
O gráfico mostra a média das amostras coletadas ao longo do tempo (20 amostras de 5 medições).
A linha verde é a média geral do processo.
As linhas vermelhas representam os limites de controle. Se algum ponto cair fora desses limites, isso indica uma variação especial (fora de controle), o que exige investigação e ação corretiva.
Controle de Variabilidade e Proporção Defeituosa#
2.1 Controle de Variabilidade do Processo (Gráfico de Controle de Desvio Padrão)#
Além de monitorar a média, é importante monitorar a variabilidade do processo. Isso nos ajuda a garantir que o processo seja consistente e confiável.
No contexto da construção civil, a variabilidade pode ser crucial:
Se a espessura das lajes de concreto não for consistente, isso pode comprometer a resistência e segurança estrutural.
Se a resistência do concreto variar muito, pode afetar a durabilidade e segurança da construção.
2.2 Gráfico de Controle de Desvio Padrão (S-chart)#
Passos:
Coletamos amostras do processo, como fizemos no gráfico de controle de média.
Calculamos o desvio padrão de cada amostra.
Calculamos os limites de controle superior (UCL) e inferior (LCL) para o desvio padrão.
Exemplo de Código - Gráfico de Controle de Variabilidade#
# Calculando o desvio padrão de cada amostra
desvios = np.std(dados, axis=1)
# Calculando a média do desvio padrão
media_desvio = np.mean(desvios)
# Calculando os limites de controle para o desvio padrão (S-chart)
UCL_S = media_desvio + 3 * np.std(desvios)
LCL_S = media_desvio - 3 * np.std(desvios)
# Plotando o gráfico de controle do desvio padrão
plt.figure(figsize=(10, 6))
plt.plot(desvios, marker='o', label="Desvio padrão das amostras")
plt.axhline(media_desvio, color='green', linestyle='--', label="Média do Desvio Padrão")
plt.axhline(UCL_S, color='red', linestyle='--', label="Limite Superior de Controle (UCL)")
plt.axhline(LCL_S, color='red', linestyle='--', label="Limite Inferior de Controle (LCL)")
plt.title("Gráfico de Controle de Desvio Padrão (S-chart) - Variação na Espessura do Concreto")
plt.xlabel("Amostra")
plt.ylabel("Desvio Padrão (mm)")
plt.legend()
plt.show()
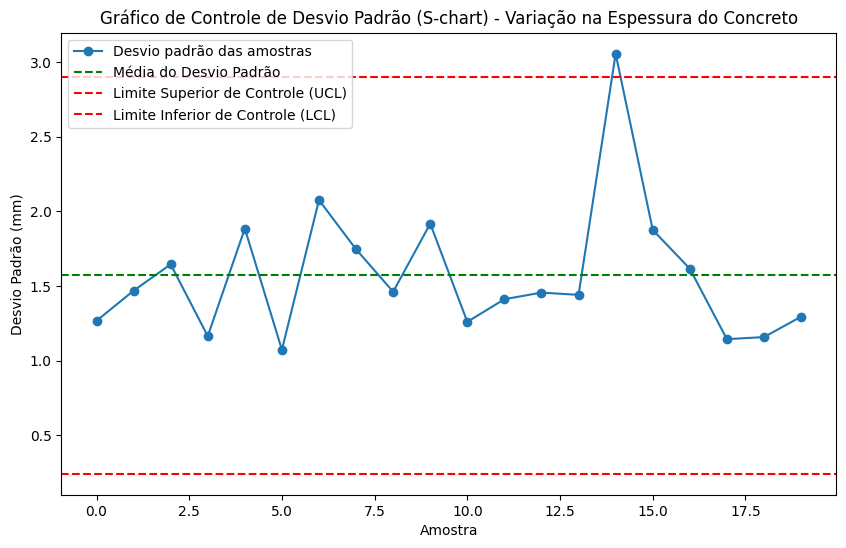
Explicação do gráfico:
O gráfico mostra como o desvio padrão (variabilidade) das amostras varia ao longo do tempo.
Se algum ponto ultrapassar os limites de controle, o processo deve ser ajustado para reduzir a variabilidade.
2.3 Controle de Proporção Defeituosa (p-chart)#
No controle de processos, podemos também monitorar a proporção de defeituosos em um lote de produção. Na construção civil, isso pode ser relacionado à quantidade de concreto que não atendeu aos requisitos de resistência ou espessura mínima.
Passos:
Definimos uma quantidade de itens a serem inspecionados (ex: 100 blocos de concreto).
Contamos quantos itens apresentam defeitos.
Calculamos a proporção de defeituosos para cada amostra e, a partir disso, geramos um gráfico de controle para a proporção defeituosa.
Exemplo de Código - Gráfico de Controle de Proporção Defeituosa#
# Definindo o número total de itens e defeituosos
total_itens = 100
defeituosos = 5
proporcao_defeituosos = defeituosos / total_itens
# Gerando 20 amostras de defeituosos
amostras_defeituosos = np.random.binomial(n=total_itens, p=proporcao_defeituosos, size=20)
proporcao_amostras = amostras_defeituosos / total_itens
# Calculando os limites de controle para o p-chart
p_barra = np.mean(proporcao_amostras)
UCL_p = p_barra + 3 * np.sqrt((p_barra * (1 - p_barra)) / total_itens)
LCL_p = p_barra - 3 * np.sqrt((p_barra * (1 - p_barra)) / total_itens)
# Plotando o gráfico de controle de proporção defeituosa
plt.figure(figsize=(10, 6))
plt.plot(proporcao_amostras, marker='o', label="Proporção de defeituosos")
plt.axhline(p_barra, color='green', linestyle='--', label="Proporção média")
plt.axhline(UCL_p, color='red', linestyle='--', label="Limite Superior de Controle (UCL)")
plt.axhline(LCL_p, color='red', linestyle='--', label="Limite Inferior de Controle (LCL)")
plt.title("Gráfico de Controle de Proporção Defeituosa (p-chart) - Concreto com Defeitos")
plt.xlabel("Amostra")
plt.ylabel("Proporção de defeituosos")
plt.legend()
plt.show()
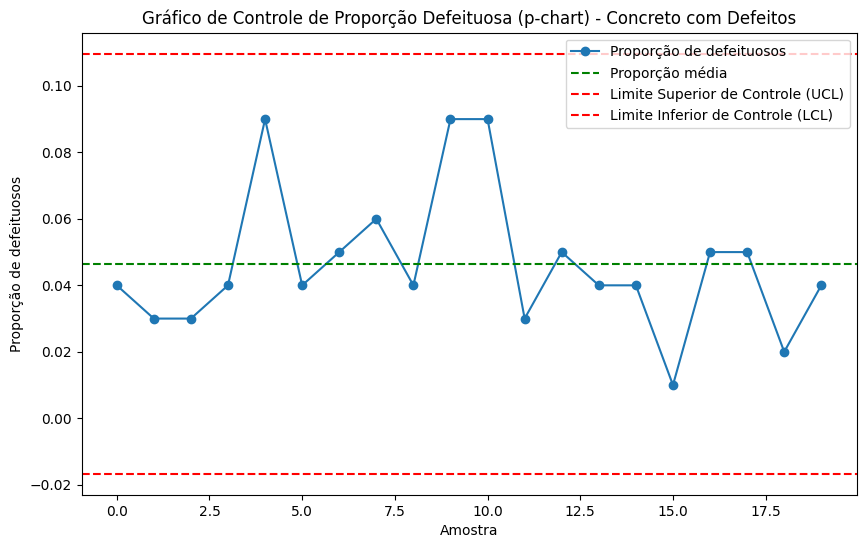
Explicação do gráfico:
O gráfico mostra a proporção de defeituosos em cada amostra de concreto (como blocos ou peças de concreto).
A linha verde indica a proporção média de defeituosos, enquanto as linhas vermelhas indicam os limites de controle.
Se a proporção de defeituosos em uma amostra cair fora dos limites de controle, isso sugere que o processo está fora de controle e deve ser investigado para identificar e corrigir a causa da variação.
Resumo#
CEP (Controle Estatístico de Processos) é uma metodologia que ajuda a monitorar e controlar a qualidade de um processo. Ele visa detectar variações especiais e minimizar variações comuns para garantir que o processo permaneça estável e dentro das especificações.
Variação Comum: Variações naturais que ocorrem dentro do processo.
Variação Especial: Variações causadas por fatores externos ou anômalos.
Gráficos de Controle ajudam a visualizar essas variações e identificar quando o processo está fora de controle.
Exemplos aplicados na construção civil incluem o controle de resistência do concreto e a espessura do concreto.
Gráfico de Controle de Desvio Padrão (S-chart): Usado para monitorar a variabilidade de um processo. No exemplo da construção civil, isso poderia ser aplicado ao controle da espessura do concreto ou à variação na resistência.
Gráfico de Controle de Proporção Defeituosa (p-chart): Usado para monitorar a proporção de defeituosos em um processo. No caso da construção civil, pode ser usado para monitorar a proporção de peças de concreto que não atendem às especificações de resistência ou qualidade.
Aplicações Práticas e Conclusão#
O Controle Estatístico de Processos (CEP) é amplamente utilizado na construção civil para garantir a qualidade e a segurança das construções. Processos como a mistura de concreto, a resistência do concreto e a espessura das lajes são monitorados para garantir que o trabalho esteja dentro dos padrões exigidos.
Por exemplo:
Monitoramento da resistência do concreto: Ao controlar a resistência média do concreto (gráfico de média) e a variabilidade (gráfico de desvio padrão), podemos garantir que o concreto utilizado nas fundações ou lajes de uma obra tenha qualidade suficiente para suportar as cargas a que será submetido.
Controle de defeituosos: Usar um gráfico de proporção defeituosa (p-chart) para controlar a proporção de blocos de concreto defeituosos ajuda a manter a qualidade durante o processo de produção e fabricação.
O CEP não só identifica problemas em um processo, mas também ajuda a prevenir falhas por meio da monitorização constante da qualidade. Usar essas ferramentas ajuda a reduzir desperdícios, melhorar a eficiência e garantir a segurança e qualidade das obras. Esses conceitos têm um grande impacto na qualidade e no controle dos processos na engenharia, especialmente em áreas tão críticas como a construção civil.
